16진법이란?
영어로는 hexadecimal(헥사데시멀), 보통은 줄여서 hex(헥사 또는 헥스)라고 하며, 컴퓨터 분야에서는 이진법과 마찬가지로 가장 많이 사용하는 표현 방식인데요. 이전에 포스팅했던 이진법은 0과 1을 표현하는 비트로 이루어진 표현 방식이였는데 이번 16진법은 숫자 10개(0-9)와 영어 알파벳 6개(a-f), 총 16개의 문자로 이루어져 있으며, 이 문자들은 각각 0에서 15까지의 값을 표현하고 있는데 0-9는 그냥 0-9를 표현 하고, 알파벳은 각자...
a = 10, b = 11, c = 12, d = 13, e = 14, f = 15의 값 표현하고 있습니다. (대문자도 의미는 같습니다)
여기서 한가지 먼저 집고 넘어가자면,16진법은 16개의 문자로 16을 넘지 않는 0-15까지 수를 표현하는 문자, 10진법은 10개의 문자로 10을 넘지 않는 0-9까지 수를 표현하는 문자, 2진법도 2개의 문자로 2를 넘지않는 0-1의 문자로 수를 표현하고 있습니다. 그런데 여기서 혹시, 10진법이 0-9까지를 표현하는 수로 이루어져 있다고 말씀드렸는데...
'10진수는 100도 있고 1560도 있고 표현할 수 있는 수가 많은데 왜 9까지 밖에 표현을 못한다고 하는거야?' 라고 생각하신다면, 위에 예시인 100, 1560은 모두 0-9사이의 문자로 이루어져 있으며, 당장 10을 표현할려고 해도 1과 0두개로 표시해야 하는 겁니다.
다시 16진법으로 돌아와서, 16진법으로 표현한 16진수는 보통 '0x'라는 문자를 앞에 붙여 사용하며, 내가 지금쓴 글이 16진수임을 알려주는 식별자와 같습니다. 예를 들어 몇가지 써보면... 0x00, 0x2f, 0x015d, 0xb1a4 등 '0x'를 앞에 붙이며 그 다음 특징으로는 보통 '0x'뒤에 문자를 2개 씩 붙여서 쓰는데, 제가 쓴 예시를 0x를 빼고보면 00, 2f, 015d, b1a4로 두 글자씩 쓴다는 겁니다. 이는 2진법과 관련이 있으며, 이 내용은 아래에서 따로 설명하겠습니다.
16진법의 10진수변환
16진법은 0에서 15까지의 수를 표현하는 0 - 9 및 a - f까지의 문자로 이루어져 있으며, 만약 10을 표현할려면 0x0a, 13을 표현 할려면 0x0d, 15를 표현할려면 0x0f라고 써야 하며, 만약 '15를 넘어가는 16를 표현하고 싶다'라고 한다면 0x10이라고 표현을 하면 됩니다. 이것은 자리 수를 넘기는 행위이며, 10진수의 숫자 구(9)보다 하나 큰 수인 십을... 10의 자리를 1올리고 1의 자리를 0이라고 바꿔 '10'이라고 하는 것과 같습니다. 이를 정리하면...
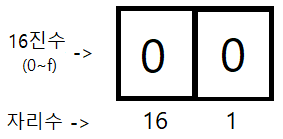
위 이미지와 같이 정리할 수 있으며, 오른쪽 끝에 칸의 자리수를 1로 시작해서 왼쪽으로 한칸 이동할 때 마다 16배씩 증가하며, 각 칸에는 0~f(15)의 값이 들어갈 수 있습니다. 이 때 위에 예시로 든 0x0f, 0x10의 값을 수식을 써서 표현하면...
0x0f는 16의 자리가 0, 1의 자리는 f(15)이므로 [16 * 0] + [1 * f(15)]를 계산해서 15,
0x10은 16의 자리가 1, 1의 자리는 0으로 [16 * 1] + [1 * 0]을 계산해서 16 으로 계산됩니다.
그렇다면, 16진법으로 0xd7이라고하면 어떤 값이 나올까요?

그냥 똑같이 하시면 됩니다. 16의 자리가 d, 1의 자리가 7이므로 [16 * d(13)] + [1 * 7]을 계산해서 215가 나옵니다.
16진법과 2진법 변환
이 글을 읽기전 이진법을 모르시는 분들은 이진법 포스팅을 보고오시기 바랍니다. 이진법 포스팅
위 글에서 잠깐... 16진법은 0x00, 0xb1a4 처럼 문자를 두개씩 쓰는 것이 2진법과 관련이 있다고 했는데요. 이는 사실 컴퓨터의 바이트랑 연관되어 있습니다.
바이트에 관해 잠깐 설명드리면 바이트(byte)는 8bit의 단위이며, 1byte는 = 8bit인데요. 컴퓨터의 가장 작은 최소단위는 비트이지만, 일반적으로 용량같은 단위를 표시할 때는 킬로바이트(KB), 메가바이트(MB), 기가바이트(GB)등 byte라는 단위를 많이 사용합니다.
이렇게 컴퓨터는 바이트(byte)라는 단위를 많이 사용하는데, 이는 16진법도 마찬가지 입니다. 16진수의 0~f까지의 값은 이진수 보면 4bit로 표현이 가능하고 이 값을 두개 사용하는 0x00, 0xd7, 0xff와 같은 16진수들은 8bit 즉 한개의 바이트를 나타내는 것이죠. 그렇다면 16진수를 2진수로 바꾸는 방법도 알아봅시다.
16진수의 0~f는 십진수로 0~15를 표현한다고 알려드렸는데, 4개의 bit도 0~15를 표현할 수 있습니다. 즉 1대 1 매칭을 하면 0~f를 이진수로 바꿀수 있게 되는 것이며, 0xca같이 16진수가 두개가 들어가는 건 똑같이 c랑 a을 각각 매칭시켜주면 끝나는 것인데요.
| 16진수 | 2진수 | 16진수 | 2진수 |
| 0 | 0000 | 8 | 1000 |
| 1 | 0001 | 9 | 1001 |
| 2 | 0010 | a | 1010 |
| 3 | 0011 | b | 1011 |
| 4 | 0100 | c | 1100 |
| 5 | 0101 | d | 1101 |
| 6 | 0110 | e | 1110 |
| 7 | 0111 | f | 1111 |
위 표가 0~15를 표현하는 16진수와 2진수의 표 인데요. 이표를 기준으로 0xca을 이진수로 변환해보면....
16진수 c는 2진수로 1100, 16진수 a은 2진수로 1010 으로 16진수 0xca은 2진수로 1100 1010로 쓰면 됩니다.
0~f까지의 값을 2진수로 매칭만 시켜주면 참 쉽죠?
그럼 16진수 0xca와 2진수 1100 1010이 정말 같은 값인지 확인하기 위해 둘 다 10진수로 변환해서 같은지 확인해봅시다.

먼저 16진수 0xca부터 10진수로 변환하면 C는 12고 a는 10이죠 그럼.... [16 * c(12)] + [1 * a(10)]으로 계산해서 202가 나오고,

이제 이진수인 1100 1010을 10진수로 변환해보면, 의미 없는 0자리는 빼고 [128] + [64] +[8] + [2] 로 202가 나옵니다. 그러므로, 0xca와 이진수 1100 1010은 서로 202로 같으며, 이는 0xca = 1100 1010 =202로 표현할 수 있습니다.
글을 마치며
사실 이번글은... 이진법 포스팅을 할 때 16진법도 같이 작성할려고 했으나, 글이 너무 길어져 가독성이 떨어질 것을 우려해이진법과 16진법으로 따로 글을 작성했는데요. 그래서 이번글 전체를 이해할려면 이진법에 대한 지식이 있어야한다는 제약이 생겼습니다....
짧게 압축하면 한 포스팅에도 작성할 수 있을 것 같은데... 일단 죄송합니다. 가능하면 보고오시길 추천드립니다.
'컴퓨터' 카테고리의 다른 글
| 이진법(binary) (0) | 2024.01.17 |
|---|